AG Kombinatorische Optimierung

Complex Scheduling Problems

(V4+Ü2)

Inhalt

Es werden ressourcenbeschränkte Projektplanungsprobleme und effiziente Lösungsalgorithmen (MIPs, Heuristiken, lokale Suche, genetische Algorithmen, constraint propagation, lineare Programmierung, Branch-and-Bound-Algorithmen) behandelt.

RCPSP

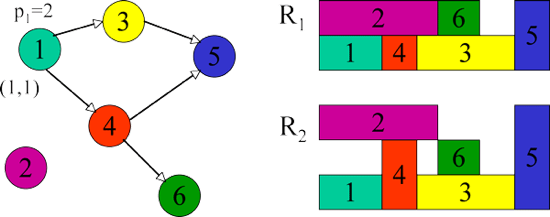
Gegeben ist eine Menge von Aktivitäten (Jobs), die für eine bestimmte Zeitdauer bearbeitet werden müssen. Während ihrer Bearbeitung werden Ressourcen (Maschinen, Personen, Energie, Geld) benötigt, die nur mit einer begrenzten Kapazität zur Verfügung stehen. Das Hauptproblem besteht darin, einen Plan zu finden, bei dem alle Ressourcenkapazitäten eingehalten werden und eine bestimmte Zielfunktion minimiert wird.

Beispiele für solche Probleme finden sich in der Produktionsplanung, Software-Entwicklung, Schulstundenplanung, Eisenbahnscheduling, Sportligaplanung, usw.

Stichworte:

RCPSP (resource-constrained project scheduling problem), einige Verallgemeinerungen und Anwendungen
Heuristiken für das RCPSP
Constraint propagation für das RCPSP
Untere Schranken für das RCPSP
Branch-and-Bound Algorithmen für das RCPSP

Literatur

Baptiste, P., Le Pape, C., Nuijten, W. (2001): Constraint-Based Scheduling -- Applying Constraint Programming to Scheduling Problems, International Series in Operations Research and Management Science, Vol. 39, Kluwer.
Brucker, P., Knust, S. (2012): Complex Scheduling, 2. Auflage, Springer.
Demeulemeester, E., Herroelen, W. (2002): Project Scheduling, A Research Handbook, Kluwer.
Dorndorf, U. (2002): Project Scheduling with Time Windows - From Theory to Applications, Springer.
Neumann, K., Schwindt, C., Zimmermann, J. (2003): Project Scheduling with Time Windows and Scarce Resources -- Temporal and Resource-Constrained Project Scheduling with Regular and Nonregular Objective Functions, Springer.

Materialien

Überblick (PDF) (Überblick, Lernziele)
PSPLIB
ZIB Optimization Suite (enthält Zimpl, SCIP und SoPlex)

Teilnahme

Die Veranstaltung ist vorgesehen für M.Sc. ab dem 1. Semester. Grundkenntnisse aus der kombinatorischen Optimierung werden vorausgesetzt.

Schein

Voraussetzung für den Erwerb eines Scheins zur Veranstaltung ist die regelmäßige Teilnahme an den Übungen, die erfolgreiche Bearbeitung der praktischen Übungen und die erfolgreiche Absolvierung einer Prüfung (Klausur) am Ende des Semesters. Prüfungsrelevant sind alle Kapitel der Vorlesung sowie die Themen aus den Übungen.