Introduction
Next: Iterative-Deepening Search
Up: AIDA* - Asynchronous Parallel
Previous: AIDA* - Asynchronous Parallel
Heuristic search is one of the most important techniques
for problem solving in Artificial Intelligence and Operations Research.
Since search algorithms usually exhibit exponential run-time,
and sometimes also exponential space complexity,
the design of efficient parallel searching methods is of obvious interest.
The backtracking approaches used in AI and OR
benefit from a wealth of powerful heuristics that
eliminate unnecessary states in the search space without affecting the final result.
The most prominent methods include the universal branch & bound technique
and dynamic programming,
which examine only branches that are below/above a current upper/lower bound
on the solution value.
While these schemes are successfully applied in many problem domains,
they do not work in domains with
- low solution density,
- high heuristic branching factor,
- poor initial upper/lower bounds on the optimal solution value.
Typical examples include single-agent games like the
15-puzzle [Korf, 1985], VLSI floorplan optimization [Wimer et al., 1988],
and some variants of the cutting stock problem [Morabito et al., 1992].
For this kind of applications, there exists a simple and efficient backtracking method,
called Iterative-Deepening A* (IDA*) [Korf, 1985],
that performs a series of independent
depth-first searches, each with the cost-bound increased by the minimal amount.
In this paper, we present AIDA*,
a parallel implementation of iterative-deepening search on
a massively parallel asynchronous MIMD system.
AIDA* is based on a data partitioning scheme, where
the different parts of the search space are processed asynchronously by
the distributed processing elements.
A simple, but effective task attraction scheme combined with a weak synchronization
mechanism ensures high processor utilization and good scalability
for up to more than a thousand processors.
Running on a 1024 processor transputer system,
we achieved a speedup of 807 on twentyfive problem instances of the
15-puzzle, corresponding to an efficiency of 79%.
Using Korf's [1985] random problem instances as a benchmark suite,
AIDA* runs more than five times as fast as the fastest SIMD implementation,
SIDA* by Powley et al. [1993], which was implemented
on a CM-2 with 32K processing elements.
While such a comparison might seem unfair, because
a single CM-2 processing element is about 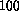 times slower than the
T805 transputers of our system,
there are 32 times more processing elements in the CM-2.
Hence one would expect our transputer program to run three times
faster.
However, we achieved a time improvement by a factor of 5.7,
due to faster work-load balancing and almost zero synchronization costs.
times slower than the
T805 transputers of our system,
there are 32 times more processing elements in the CM-2.
Hence one would expect our transputer program to run three times
faster.
However, we achieved a time improvement by a factor of 5.7,
due to faster work-load balancing and almost zero synchronization costs.
In the following, we first discuss the basic ideas of sequential IDA*,
give a brief overview about previous parallel approaches,
and present the AIDA* algorithm.
Most of the paper is devoted to the discussion of our empirical performance results,
including an analysis of the various overheads.
Next: Iterative-Deepening Search
Up: AIDA* - Asynchronous Parallel
Previous: AIDA* - Asynchronous Parallel
Volker Schnecke
Mon Dec 19 17:27:56 MET 1994
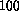 times slower than the
T805 transputers of our system,
there are 32 times more processing elements in the CM-2.
Hence one would expect our transputer program to run three times
faster.
However, we achieved a time improvement by a factor of 5.7,
due to faster work-load balancing and almost zero synchronization costs.
times slower than the
T805 transputers of our system,
there are 32 times more processing elements in the CM-2.
Hence one would expect our transputer program to run three times
faster.
However, we achieved a time improvement by a factor of 5.7,
due to faster work-load balancing and almost zero synchronization costs.