Conclusions and Future Research
Next: Appendix: All-Solutions-Case Data
Up: AIDA* - Asynchronous Parallel
Previous: Termination Detection
In this paper, we presented a universal scheme for asynchronous parallel
iterative-deepening search on massively parallel MIMD systems.
Any sequential iterative-deepening algorithm can be linked to
our generic AIDA* routines without much modification.
Compared to a similar parallel MIMD scheme by
Kumar and Rao [1990], our method is more general
and obeys less communication overhead,
especially on MIMD systems with a large diameter.
Moreover, AIDA* proved to be scalable for
more than one thousand processors with a high efficiency.
For the `first-solution-case',
we solved Korf's [1985] hundred puzzle instances
in 24 minutes, which is 5.7 times faster than SIDA*
[Powley et al., 1993] running on a 32K CM-2.
Comparing SIDA*'s theoretical speed of 32K processors 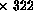 nodes/sec
nodes/sec 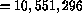 nodes/sec for the whole system with AIDA*'s
theoretical speed of 1024 processors
nodes/sec for the whole system with AIDA*'s
theoretical speed of 1024 processors  nodes/sec
nodes/sec 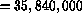 nodes/sec
for our whole system,
it is evident, that our MIMD approach makes better use of the processors.
This is a remarkable result, considering that our faster machine solves the
smallest 70 problems in less than 10 seconds each.
Here, losses due to initialization are most pregnant.
On the other hand, it is a more ambitious task to keep all processors of a SIMD
machine working on relevant parts of the search space.
nodes/sec
for our whole system,
it is evident, that our MIMD approach makes better use of the processors.
This is a remarkable result, considering that our faster machine solves the
smallest 70 problems in less than 10 seconds each.
Here, losses due to initialization are most pregnant.
On the other hand, it is a more ambitious task to keep all processors of a SIMD
machine working on relevant parts of the search space.
Our future work includes the solution of the 19-puzzle,
where all heuristics that are known up to date, must be put together
to obtain a solution within reasonable time limits.
At the present time, we have solved 20 smaller problems of 100 random 19-puzzle instances with an average runtime of 34 minutes on the
1024 processor system.
VLSI floorplan optimization [Wimer et al., 1988]
is another practical application,
which we intend to solve with AIDA*.
problems of 100 random 19-puzzle instances with an average runtime of 34 minutes on the
1024 processor system.
VLSI floorplan optimization [Wimer et al., 1988]
is another practical application,
which we intend to solve with AIDA*.
Volker Schnecke
Mon Dec 19 17:27:56 MET 1994
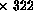 nodes/sec
nodes/sec 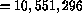 nodes/sec for the whole system with AIDA*'s
theoretical speed of 1024 processors
nodes/sec for the whole system with AIDA*'s
theoretical speed of 1024 processors  nodes/sec
nodes/sec 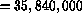 nodes/sec
for our whole system,
it is evident, that our MIMD approach makes better use of the processors.
This is a remarkable result, considering that our faster machine solves the
smallest 70 problems in less than 10 seconds each.
Here, losses due to initialization are most pregnant.
On the other hand, it is a more ambitious task to keep all processors of a SIMD
machine working on relevant parts of the search space.
nodes/sec
for our whole system,
it is evident, that our MIMD approach makes better use of the processors.
This is a remarkable result, considering that our faster machine solves the
smallest 70 problems in less than 10 seconds each.
Here, losses due to initialization are most pregnant.
On the other hand, it is a more ambitious task to keep all processors of a SIMD
machine working on relevant parts of the search space.