Applications
Next: Parallel Approaches
Up: AIDA* - Asynchronous Parallel
Previous: Iterative-Deepening Search
Typical application domains for IDA* search include VLSI floorplan optimization,
some variants of the cutting stock problem and single-agent games like the 15-puzzle.
These problems may be characterized by a high heuristic branching factor,
a low solution density and poor information about bounds that can be used
to prune the search tree.
We tested the performance of our parallel AIDA* algorithm on one hundred
randomly generated problem instances [Korf, 1985] of the 15-puzzle.
In its more general 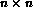 extension, this puzzle is known to be
extension, this puzzle is known to be
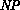 -complete [Ratner and Warmuth, 1986].
While exact statistics on solving the smaller 8-puzzle are known [Reinefeld, 1993],
the 15-puzzle spawns a search space of
-complete [Ratner and Warmuth, 1986].
While exact statistics on solving the smaller 8-puzzle are known [Reinefeld, 1993],
the 15-puzzle spawns a search space of
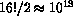 states, which cannot be exhaustively examined.
Using IDA*, an average of
states, which cannot be exhaustively examined.
Using IDA*, an average of 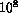 node expansions are needed
to obtain a first solution with the popular Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.
node expansions are needed
to obtain a first solution with the popular Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.
Volker Schnecke
Mon Dec 19 17:27:56 MET 1994
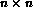 extension, this puzzle is known to be
extension, this puzzle is known to be
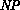 -complete [Ratner and Warmuth, 1986].
While exact statistics on solving the smaller 8-puzzle are known [Reinefeld, 1993],
the 15-puzzle spawns a search space of
-complete [Ratner and Warmuth, 1986].
While exact statistics on solving the smaller 8-puzzle are known [Reinefeld, 1993],
the 15-puzzle spawns a search space of
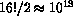 states, which cannot be exhaustively examined.
Using IDA*, an average of
states, which cannot be exhaustively examined.
Using IDA*, an average of 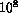 node expansions are needed
to obtain a first solution with the popular Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.
node expansions are needed
to obtain a first solution with the popular Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.