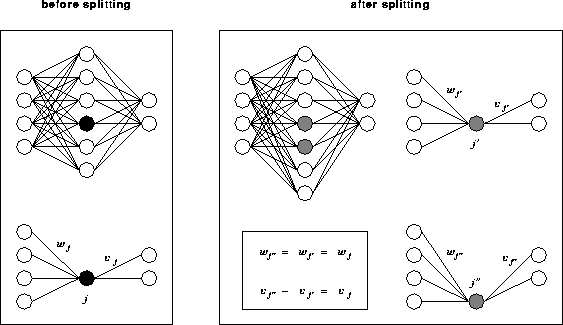
Figure 2: Modified back-propagation with neuron splitting
The optimal configuration of a FMP network with its input, hidden and output layers is very difficult. The right number of hidden layers and the number of neurons within each layer is hard to find. Too many hidden neurons lead to a net that is not able to extract the function rule and takes more time for learning. With a lack in hidden neurons it is not possible to reach any error bound. Input and output layers are determined by the problem and the function that is to be approximated.
The back-propagation algorithm is used to minimize the error of the net by modifying the activation weights between the neurons. During the forward propagation the error between the nominal and the actual value is calculated. During the backward propagation the weights are modified in order to minimize this error. The basis of this method is gradient descent.
Our modified back-propagation algorithm [5] is able to increase the quality of a net by monotonic net incrementation. The training starts with a net of few hidden neurons. Badly trained neurons are split periodically while learning the training set. The old weights are distributed by chance between the two new neurons (cf. Figure 2). This is done until a maximum number of neurons within a hidden layer is reached. By training the net with the modified back-propagation algorithm a better minimum of the error is reached in shorter time.

Figure 2: Modified back-propagation with neuron splitting