References

1: Adler, I., Erera, A.L., Hochbaum, D.S., Olinick, E.V. (2002) Baseball, optimization, and the world wide web, Interfaces 32, 12-22.
2: Adriaen, M., Custers, N., Vanden Berghe, G. (2003) An agent based metaheuristic for the traveling tournament problem, Working Paper, KaHo Sint-Lieven, Gent, Belgium.
3: Aggoun, A., Vazacopoulos, A. (2004) Solving sports scheduling and timetabling problems with constraint programming, in: S. Butenko, J. Gil-Lafuente and P.M. Pardalos (eds.), Economics, Management and Optimization in Sports, Springer, 243-264.
4: Alarcón, F., Duran, G., Guajardo, M. (2014) Referee assignment in the Chilean football league using integer programming and patterns, International Transactions in Operational Research 21, 415-438.
5: Alarcón, F., Duran, G., Guajardo, M., Miranda, J., Munoz, H., Ramirez, L., Ramirez, M., Saure, D., Siebert, M., Souyris, S., Weintraub, A., Wolf-Yadlin, R., Zamoranoa, G. (2017) Operations Research transforms the scheduling of Chilean soccer leagues and South American world cup qualifiers, Interfaces 47, 52-69.
6: Anagnostopoulos, A., Michel, L., van Hentenryck, P., Vergados, Y. (2003) A simulated annealing approach to the traveling tournament problem, Proceedings CPAIOR'03, Montreal.
7: Anagnostopoulos, A., Michel, L., van Hentenryck, P., Vergados, Y. (2006) A simulated annealing approach to the traveling tournament problem, Journal of Scheduling 9, 177-193.
8: Anderson, I. (1997) Combinatorial Designs and Tournaments, Oxford Lecture Series in Mathematics and Its Applications.
9: Anderson, I. (1999) Balancing carry-over effects in tournaments, in: Combinatorial designs and their applications, Chapman & Hall/CRC Res. Notes Math., 403, Boca Raton, FL, 1-16.
10: Anderson, I., Bailey, R.A. (1997) Completeness properties of conjugates of Latin squares based on groups, and an application to bipartite tournaments, Bulletin of the Institute of Combinatorics and its Applications 21, 95-99.
11: Anderson, I., Ferguson, C. (2004) Training schedules balanced for carryover effects, Bulletin of the Institute of Combinatorics and its Applications 40, 5-12.
12: Andreu, R., Corominas, A. (1989) SUCCESS92: a DSS for scheduling the olympic games, Interfaces 19, 1-12.
13: Araújo, A., Boeres, M.C., Rebello, V.E., Ribeiro, C.C., Urrutia, S. (2007) Exploring grid implementations of parallel cooperative metaheuristics: A case study for the mirrored traveling tournament problem, in: K.F. Doerner, M. Gendreau, P. Greistorfer, W. Gutjahr, R.F. Hartl (eds.), Metaheuristics: Progress in Complex Systems Optimization, Springer, 297-322.
14: Armstrong, J., Willis, R.J. (1993) Scheduling the cricket World Cup – a case-study, Journal of the Operational Research Society 44, 1067-1072.
15: Atan, T., Çavdaroğlu, B. (2018) Minimization of rest mismatches in round robin tournaments, Computers and Operations Research 99, 78-89.
16: Ball, B.C., Webster, D.B. (1977) Optimal scheduling for even-numbered team athletic conferences, AIIE Transactions 9, 161-169.
17: Bar-Noy, A., Moody, D. (2006) A tiling approach for fast implementation of the traveling tournament problem, in: E. Burke and H. Rudova (eds.), PATAT 2006, Proceedings, 367-369.
18: Bartsch, T. (2001) Sportligaplanung – Ein Decision Support System zur Spielplanerstellung (in German), Deutscher Universitätsverlag, Wiesbaden.
19: Bartsch, T., Drexl, A. (2001) Fussball und Operations Research – Attraktive Spielpläne aus dem Computer (in German), OR News 13, 10-14.
20: Bartsch, T., Drexl, A. (2006) Fussballbundesliga-Spielpläne aus dem Computer (in German), OR News Sonderausgabe, 125-129.
21: Bartsch, T., Drexl, A., Kröger, S. (2006) Scheduling the professional soccer leagues of Austria and Germany, Computers and Operations Research 33, 1907-1937.
22: Bean, J.C., Birge, J.R. (1980) Reducing travelling costs and player fatigue in the national basketball association, Interfaces 10, 98-102.
23: Beintema, M.B., Bonn, J.T., Fitzgerald, R.W., Yucas, J.L. (1998) Orderings of finite fields and balanced tournaments, Ars Combinatoria 49, 41-48.
24: Benoist, T., Laburthe, F., Rottembourg, B. (2001) Lagrange relaxation and constraint programming collaborative schemes for travelling tournament problems, Proceedings CPAIOR'01, Wye College (Imperial College), Ashford, Kent UK.
25: Bernholt, T., Gülich, A. (2000) Anwendung von Komplexitätstheorie und effizienten Algorithmen auf die Fussballbundesliga (in German), Diplomarbeit, Universität Dortmund.
26: Bernholt, T., Gülich, A., Hofmeister, T., Schmitt, N., Wegener, I. (2002) Komplexitätstheorie, effiziente Algorithmen und die Bundesliga (in German), Informatik Spektrum 16, 488-502.
27: Bhattacharyya, R. (2016) Complexity of the unconstrained traveling tournament problem, Operations Research Letters 44, 649-654.
28: Birge, J.R. (2004) Scheduling a professional sports league in Microsoft Excel: Showing students the value of good modeling and solution techniques, INFORMS Transactions on Education 5.
29: Blest, D.C., Fitzgerald, D.G. (1988) Scheduling sports competitions with a given distribution of times, Discrete Applied Mathematics 22, 9-19.
30: Bonomo, F., Cardemil, A., Duran, G., Marenco, J., Saban, D. (2012) An application of the traveling tournament problem: the Argentine volleyball league, Interfaces 42, 245-259.
31: Brandao, F., Pedroso, J.P. (2014) A complete search method for the relaxed traveling tournament problem, EURO Journal on Computational Optimization, 2, 77-86.
32: Briskorn, D. (2006) Scheduling sport leagues using branch-and-price, in: E. Burke and H. Rudova (eds.), PATAT 2006, Proceedings, 367-369.
33: Briskorn, D. (2007) Sport leagues scheduling: models, combinatorial properties, and optimization algorithms, Ph.D. thesis, Christian-Albrechts-Universität Kiel, Lecture Notes in Economics and Mathematical Systems, Vol. 603, Springer.
34: Briskorn, D. (2008) Feasibility of home-away-pattern sets for round robin tournaments, Operations Research Letters 36, 283-284.
35: Briskorn, D. (2009) Combinatorial properties of strength groups in round robin tournaments, European Journal of Operational Research 192, 744-754.
36: Briskorn, D. (2009) A branching scheme for minimum cost tournaments with regard to real world constraints, Report 643, Institut für Betriebswirtschaftslehre, Universität Kiel.
37: Briskorn, D., Drexl, A. (2009) A branch-and-price algorithm for scheduling sport leagues, Journal of the Operational Research Society 60, 84-93.
38: Briskorn, D., Drexl, A. (2009) IP models for round robin tournaments, Computers and Operations Research 36, 837-852.
39: Briskorn, D., Drexl, A. (2009) A branching scheme for finding cost-minimal round robin tournaments, European Journal of Operational Research 197, 68-76.
40: Briskorn, D., Drexl, A., Spieksma, F.C.R. (2010) Round tobin tournaments and three index assignments, 4OR 8, 365-374.
41: Briskorn, D., Horbach, A. (2012) A Lagrangian approach for minimum cost single round robin tournaments, Computers and Operations Research 39, 718-727.
42: Briskorn, D., Knust, S. (2010) Constructing fair sports league schedules with regard to strength groups, Discrete Applied Mathematics 158, 123-135.
43: Brouwer, A.E., Post, G., Woeginger, G.J. (2008) Tight bounds for break minimization, Journal of Combinatorial Theory (A) 115, 1065-1068.
44: Buiteveld, B., van Holland, E., Post, G., Smit, D. (2014) Round-robin tournaments with homogenous rounds, Annals of Operations Research 218, 115-128.
45: Burke, E.K., Werra, D. de, Landa Silva, J.D., Raess, C. (2004) Applying heuristic methods to schedule sports competitions on multiple venues, Proceedings PATAT 2004, Pittsburgh, USA, 441-444.
46: Burrows, W., Tuffley, C. (2015) Maximising common fixtures in a round robin tournament with two divisions, Australasian Journal of Combinatorics 63, 153-169.
47: Cain, W.O. (1977) The computer-aided heuristic approach used to schedule the major league baseball clubs, in: S.P. Ladany and R.E. Machol (eds.), Optimal Strategies in Sports, North Holland, Amsterdam, 33-41.
48: Campbell, R.T., Chen, D.-S. (1976) A minimum distance basketball scheduling problem, in: R.E. Machol, S.P. Ladany and D.G. Morrison (eds.), Management Science in Sports, 15-25.
49: Carlsson, M., Johansson, M., Larson, J. (2017) Scheduling double round-robin tournaments with divisional play using constraint programming, European Journal of Operational Research 259, 1180-1190.
50: Carvalho, M.A.M. de, Loreno , L.A.N. (2012) New models for the mirrored traveling tournament problem, Computers and Industrial Engineering 63, 1089-1095.
51: Çavdaroğlu, B., Atan, T. (2020) Determining matchdays in sports league schedules to minimize rest differences, Operations Research Letters 48, 209-216.
52: Çavdaroğlu, B., Atan, T. (2022) Integrated break and carryover effect minimization, Journal of Scheduling 25, 705-719.
53: Cechlarova, K., Potpinkova, E., Schlotter, I. (2016) Refining the complexity of the sports elimination problem, Discrete Applied Mathematics 199, 172-186.
54: Chandrasekharan, R.C., Toffolo, T.A.M., Wauters, T. (2019) Analysis of a constructive matheuristic for the traveling umpire problem, Journal of Quantitative Analysis in Sports 15, 41-57.
55: Cheung, K.K.H. (2008) Solving mirrored traveling tournament problem benchmark instances with eight teams, Discrete Optimization 5, 138-143.
56: Cheung, K.K.H. (2009) A Benders approach for computing lower bounds for the mirrored traveling tournament problem, Discrete Optimization 6, 189-196.
57: Cocchi, G., Galligari, A., Nicolino, F.P., Piccialli, V., Schoen, F., Sciandrone, M. (2018) Scheduling the Italian National Volleyball Tournament, Interfaces 48, 271-284.
58: Colbourn, C.J. (1983) Embedding partial Steiner triple systems is NP-complete, Journal of Combinatorial Theory (A) 35, 100-105.
59: Colbourn, C.J. (1984) The complexity of completing partial Latin squares, Discrete Applied Mathematics 8, 25-30.
60: Colbourn, C.J., Dinitz, J.H. (2006) Handbook of Combinatorial Designs, 2nd edition, CRC Press.
61: Corriveau, J. (1988) Enumeration of balanced tournament designs, Ars Combinatoria 25, 93-105.
62: Costa, D. (1995) An evolutionary tabu search algorithm and the NHL scheduling problem, INFOR 33, 161-178.
63: Costa, F.N., Urrutia, S., Ribeiro, C.C. (2012) An ILS heuristic for the traveling tournament problem with predefined venues, Annals of Operations Research 194, 137-150.
64: Cotta, C., Dotu, I., Fernandez, A.J., van Hentenryck, P. (2006) Scheduling social golfers with memetic evolutionary programming, Lecture Notes in Computer Science 4030, Springer, 150-161.
65: Craig, S., While, L, Barone, L. (2009) Scheduling for the National Hockey League using a multi-objective evolutionary algorithm, Lecture Notes in Artificial Intelligence 5866, Springer, 381-390.
66: Crauwels, H., Van Oudheusden, D. (2003) Ant colony optimization and local improvement, Workshop of Real-Life Applications of Metaheuristics, Antwerp, Belgium.
67: Davari, M., Goossens, D., Beliën, J., Lambers, R., Spieksma, F.C.R. (2020) The multi-league sports scheduling problem, or how to schedule thousands of matches, Operations Research Letters 48, 180-187.
68: Dejonghe, T. (2004) Restructuring the Belgian professional football league: a location-allocation solution, Tijdschrift voor Economische en Sociale Geografie 95, 73-88.
69: Della Croce, F., Tadei, R., Asioli, P.S. (1999) Scheduling a round robin tennis tournament under courts and players availability constraints, Annals of Operations Research 92, 349-361.
70: Della Croce, F., Oliveri, D. (2006) Scheduling the Italian Football League: an ILP-based approach, Computers and Operations Research 33, 1963-1974.
71: Di Gaspero, L., Schaerf, A. (2007) A composite-neighborhood tabu search approach to the traveling tournament problem, Journal of Heuristics 13, 189-207.
72: Dinitz, J.H. (2004) Designing schedules for leagues and tournaments, Talk at Graph Theory Day 48, November 13, 2004.
73: Dinitz, J.H., Dinitz, M. (2005) Enumeration of balanced tournament designs on 10 points, Journal of Combinatorial Mathematics and Combinatorial Computing 52, 51-64.
74: Dinitz, J.H., Froncek, D. (2000) Scheduling the XFL, Congressus Numerantium 147, 5-15.
75: Dinitz, J.H., Froncek, D., Lamken, E.R. , Wallis, W.D. (2006) Scheduling a tournament, in: C.J. Colbourn, J.H. Dinitz (eds.), Handbook of Combinatorial Designs, CRC Press, [60].
76: Dinitz, J.H., Ling, A.C.H. (2001) The existence of referee squares, Discrete Mathematics 232, 109-112.
77: Dinitz, J.H., Stinson, D.R. (2005) On assigning referees to tournament schedules, Bulletin of the Institute of Combinatorics and its Applications 44, 22-28.
78: Dotu, I., van Hentenryck, P. (2005) Scheduling social golfers locally, Lecture Notes in Computer Science 3524, Springer, 155-167.
79: Drexl, A., Knust, S. (2007) Sports league scheduling: graph- and resource-based models, Omega 35, 465-471.
80: Duarte, A.R., Ribeiro, C.C., Urrutia, S. (2007) A hybrid ILS heuristic to the referee assignment problem with an embedded MIP strategy, Lecture Notes in Computer Science 4771, Springer, 82-95.
81: Duarte, A.R., Ribeiro, C.C., Urrutia, S., Haeusler, E.H. (2007) Referee assignment in sports leagues, Lecture Notes in Computer Science 3867, Springer, 158-173.
82: Duran, G., Duran, S., Marenco, J., Mascialino, F., Rey, P.A. (2019) Scheduling Argentina's professional basketball leagues: A variation on the relaxed travelling tournament problem, European Journal of Operational Research 275, 1126-1138.
83: Duran, G., Guajardo, M., Lopez, A., Marenco, J., Zamoranoa, G. (2021) Scheduling multiple sports leagues with travel distance fairness: An application to Argentinean youth football, INFORMS Journal on Applied Analytics 51, 136-149.
84: Duran, G., Guajardo, M., Miranda, J., Saure, D., Souyris, S., Weintraub, A., Wolf, R. (2007) Scheduling the Chilean soccer league by integer programming, Interfaces 37, 539-552.
85: Duran, G., Guajardo, M., Saure, D. (2017) Scheduling the South American Qualifiers to the 2018 FIFA World Cup by integer programming, European Journal of Operational Research 262, 1109-1115.
86: Duran, G., Guajardo, M., Weintraub, A., Wolf, R. (2009) OR & Soccer: Scheduling the Chilean league using mathematical programming, OR/MS Today 36, 42-47.
87: Duran, G., Guajardo, M., Wolf, R. (2012) Operations research techniques for scheduling Chile's second division soccer league, Interfaces 42, 273-285.
88: Duran, G., Noronha, T.F., Ribeiro, C.C., Souyris, S., Weintraub, A. (2006) Branch-and-cut for a real-life highly constrained soccer tournament scheduling problem, in: E. Burke and H. Rudova (eds.), PATAT 2006, Proceedings, 398-401.
89: Easton, K. (2002) Using integer programming and constraint programming to solve sports scheduling problems, Ph.D. thesis, Georgia Institute of Technology, Atlanta.
90: Easton, K., Nemhauser, G., Trick, M. (2001) The travelling tournament problem: description and benchmarks, in: Proceedings CP'01, Lecture Notes in Computer Science 2239, Springer, 580-585.
91: Easton, K., Nemhauser, G., Trick, M. (2003) Solving the travelling tournament problem: a combined integer programming and constraint programming approach, in: E. Burke and P. De Causmaecker (eds.), PATAT 2002, Lecture Notes in Computer Science 2740, Springer, 100-109.
92: Easton, K., Nemhauser, G., Trick, M. (2004) Sports scheduling, in: J.T. Leung (ed.): Handbook of Scheduling, CRC Press, 52.1-52.19.
93: Easton, T., Parker, R.G. (2001) On completing latin squares, Discrete Applied Mathematics 113, 167-181.
94: Elf, M., Jünger, M., Rinaldi, G. (2003) Minimizing breaks by maximizing cuts, Operations Research Letters 31, 343-349.
95: Evans, J.R. (1988) A microcomputer-based decision support system for scheduling umpires in the American baseball league, Interfaces 18, 42-51.
96: Evans, J.R., Hebert, J.E., Deckro, R.F. (1984) Play ball: the scheduling of sports officials, Perspectives in Computing 4, 18-29.
97: Farmer, A., Smith, J.S., Miller, L.T. (2007) Scheduling umpire crews for professional tennis tournaments, Interfaces 37, 187-196.
98: Ferland, J.A., Fleurent, C. (1991) Computer aided scheduling for a sport league, INFOR 29, 14-25.
99: Fiallos, J., Perez, J., Sabillon, F., Licona, M. (2010) Scheduling soccer league of Honduras using integer programming, in: A. Johnson and J. Miller (eds.), Proceedings of the 2010 Industrial Engineering Research Conference, San Carlos, 2010.
100: Flatberg, T., Nilssen, E., Stlevik, M. (2009) Scheduling the topmost football leagues of Norway, Abstract 23rd EURO conference, Bonn, 240.
101: Finizio, N.J. (1993) Tournament designs balanced with respect to several bias categories, Bulletin of the Institute of Combinatorics and its Applications 9, 69-95.
102: Fleurent, C., Ferland, J.A. (1993) Allocating games for the NHL using integer programming, Operations Research 41, 649-654.
103: Fonseca, G.H., Toffolo, T.A. (2022) A fix-and-optimize heuristic for the ITC2021 sports timetabling problem, Journal of Scheduling 25, 273–286.
104: Franek, F., Froncek, D., Rosa, A. (2001) Imbalance in tournament designs, Australasian Journal of Combinatorics 23, 237-251.
105: Froncek, D., Meszka, M. (2003) Round robin tournaments with one bye and no breaks in home-away patterns are unique, in: Proceedings of the 1st International Conference on Multidisciplinary Scheduling: Theory and Applications (MISTA'03), Nottingham, UK, 331-340.
106: Froncek, D. (2001) Scheduling the Czech national basketball league, Congressus Numerantium 153, 5-24.
107: Froncek, D. (2010) Scheduling a tournament, in: Gallian, J.A. (ed.), Mathematics and Sports, Dolciani Mathematical Expositions 43, The Mathematical Association of America, 203-216.
108: Fujiwara, N., Imahori, S., Matsui, T., Miyashiro, R. (2007) Constructive algorithms for the constant distance traveling tournament problem, Lecture Notes in Computer Science 3867, Springer, 135-146.
109: Garcia Tercero, L., Van Bulck, D., Nießen, F., Goossens, D. (2025) Minimal and fair waiting times for single-day sports tournaments with multiple fields, Operations Research Letters 61, 107300.
110: Geinoz, A., Ekim, T., Werra, D. de (2008) Construction of balanced sports schedules using partitions into subleagues, Operations Research Letters 36, 279-282.
111: Gelling, E.N., Odeh, R.E. (1974) On 1-factorizations of the complete graph and the relationship to round robin schedules, Congressus Numerantium 9, 213-221.
112: Goerigk, M., Westphal, S. (2016) A combined local search and integer programming approach to the traveling tournament problem, Annals of Operations Research 239, 343-354.
113: Goerigk, M., Hoshino, R., Kawarabayashi, K., Westphal, S. (2014) Solving the traveling tournament problem by packing three-vertex paths, 28th AAAI Conference on Artificial Intelligence, 2271-2277.
114: Gomes, C.P., Selman, B., McAloon, K., Tretkoff, C. (1998) Randomization in backtrack search: exploiting heavy-tailed profiles for solving hard scheduling problems, in: Proceedings of the 4th International Conference on Artificial Intelligence Planning Systems (AIPS98), Pittsburgh, PA.
115: Goossens, D. (2018) Optimization in sports league scheduling: Experiences from the Belgian Pro League soccer, International Conference on Operations Research and Enterprise Systems, Communications in Computer and Information Science 884, 3-19, Springer.
116: Goossens, D., Belien, J., Spieksma, F.C.R. (2012) Comparing league formats with respect to match importance in Belgian football, Annals of Operations Research 194, 223-240.
117: Goossens, D., Spieksma, F.C.R. (2009) Scheduling the Belgian soccer league, Interfaces 39, 109-118.
118: Goossens, D., Spieksma, F.C.R. (2011) Breaks, cuts, and patterns, Operations Research Letters 39, 428-432.
119: Goossens, D., Spieksma, F.C.R. (2012) Soccer schedules in Europe: an overview, Journal of Scheduling 15, 641-651.
120: Grabau, K. (2012) Softball scheduling as easy as 1-2-3 (strikes you're out) Interfaces 42, 310-319.
121: Griggs, T.S., Rosa, A. (1996) A tour of European soccer schedules, or testing the popularity of 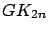$GK_{2n}$ , Bulletin of the Institute of Combinatorics and its Applications 18, 65-68.
122: Gschwind, T., Irnich, S. (2011) A note on symmetry reduction for circular traveling tournament problems, European Journal of Operational Research 210, 452-456.
123: Guajardo, M., Jörnsten, K. (2017) The stable tournament problem: matching sports schedules with preferences, Operations Research Letters 45, 461-466.
124: Guedes, A., Ribeiro, C.C. (2009) A hybrid heuristic for minimizing weighted carry-over effects in round robin tournaments, in: Proceedings of the 4th Multidisciplinary International Conference on Scheduling: Theory and Applications (MISTA'09), Dublin.
125: Guedes, A., Ribeiro, C.C. (2011) A heuristic for minimizing weighted carry-over effects in round robin tournaments, Journal of Scheduling 14, 655-667.
126: Günneç, D., Demir, E. (2019) Fair fixture: Minimizing carry-over effects in football leagues, Journal of Industrial and Management Optimization 15, 1565-1577.
127: Gusfield, D., Martel, C. (2002) The structure and complexity of sports elimination numbers, Algorithmica 32, 73-86.
128: Hamiez, J.-P., Hao, J.-K. (2001) Solving the sports league scheduling problem with tabu search, in: A.Nareyek (ed.): Local Search for Planning and Scheduling, Lecture Notes in Artificial Intelligence 2148, Springer, 24-36.
129: Hamiez, J.-P., Hao, J.-K. (2004) A linear-time algorithm to solve the sports league scheduling problem (prob026 of CSPLib), Discrete Applied Mathematics 143, 252-265.
130: Hamiez, J.-P., Hao, J.-K. (2008) Using solution properties within an enumerative search to solve a sports league scheduling problem, Discrete Applied Mathematics 156, 1683-1693.
131: Hamiez, J.-P., Hao, J.-K. (2006) Sports league scheduling: enumerative search for prob026 from CSPLib, in: F.Benhamou (ed.): CP 2006, Lecture Notes in Computer Science 4204, Springer, 716-720.
132: Haselgrove, J., Leech, J. (1977) A tournament design problem, American Mathematical Monthly 84, 198-201.
133: Hausken, M., Andersson, K., Fagerholt, K., Flatberg, T. (2013) Scheduling the Norwegian football league, International Transactions in Operational Research 20, 59-77.
134: Henz, M. (1999) Constraint-based round robin tournament planning, in: D. De Schreye (ed.), Proceedings of the International Conference on Logic Programming, Las Cruces, New Mexico, MIT Press, 545-557.
135: Henz, M. (2000) Friar Tuck - A constraint-based tournament-scheduling tool, IEEE Intelligent Systems, 15, 5-7.
136: Henz, M. (2001) Scheduling a major college basketball conference-revisited, Operations Research 49, 163-168.
137: Henz, M. (2004) Playing with constraint programming and large neighborhood search for traveling tournaments, Proceedings PATAT 2004, Pittsburgh, USA.
138: Henz, M., Müller, T., Tan, T., Thiel, S. (2000) The pairing constraint for round robin tournament scheduling, Preprint, School of Computing at the National University of Singapore.
139: Henz, M., Müller, T., Thiel, S. (2004) Global constraints for round robin tournament scheduling, European Journal of Operational Research 153, 92-101.
140: Horbach, A. (2010) A combinatorial property of the maximum round robin tournament problem, Operations Research Letters 38, 121-122.
141: Horbach, A., Bartsch, T., Briskorn, D. (2012) Using a SAT-solver to schedule sports leagues, Journal of Scheduling 15, 117-125.
142: Horton, J.D. (1989) Hamilton path tournament designs, Ars Combinatoria 27, 69-74.
143: Hoshino, R., Kawarabayashi, K. (2011) The inter-league extension of the traveling tournament application to sports scheduling, 25th AAAI Conference on Artificial Intelligence, San Francisco, USA.
144: Hoshino, R., Kawarabayashi, K. (2011) The distance-optimal inter-league schedule for Japanese Pro Baseball, ICAPS 2011 Workshop on Constraint Satisfaction Techniques for Planning and Scheduling Problems (COPLAS), Freiburg, Germany.
145: Hoshino, R., Kawarabayashi, K. (2011) The multi-round balanced traveling tournament problem, Proceedings of the 21st International Conference on Automated Planning and Scheduling (ICAPS).
146: Hoshino, R., Kawarabayashi, K. (2011) A multi-round generalization of the traveling tournament problem and its application to Japanese baseball, European Journal of Operational Research 215, 481-497.
147: Hoshino, R., Kawarabayashi, K. (2011) Scheduling bipartite tournaments to minimize total travel distance, Journal of Artificial Intelligence Research 42, 91-124.
148: Hoshino, R., Kawarabayashi, K. (2012) The linear distance traveling tournament problem, 26th AAAI Conference on Artificial Intelligence.
149: Hoshino, R., Kawarabayashi, K. (2012) Generating approximate solutions to the traveling tournament problem using a linear distance relaxation, Journal of Artificial Intelligence Research 45, 257-286.
150: Hoshino, R., Kawarabayashi, K. (2013) An approximation algorithm for the bipartite traveling tournament problem, Mathematics of Operations Research 38, 720-728.
151: Huang, H.-D., Yang, J.T., Shen, S., Horng, J.-T. (1999) An evolutionary strategy to solve sports scheduling problems, in: W. Banzhaf et al. (eds.), Proceedings of the Genetic and Evolutionary Computation Conference, Morgan Kaufmann, Los Altos, CA.
152: Hwang, F.K. (1989) How to design round-robin schedules, in: D.Z. Du, H. Guoding (eds.), Combinatorics, Computing and Complexity, Math. Appl. (Chinese series) 1, Kluwer, 142-160.
153: Ikebe, Y.T., Tamura, A. (2008) On the existence of sports schedules with multiple venues, Discrete Applied Mathematics 156, 1694-1710.
154: Imahori, S., Matsui, T., Miyashiro, R. (2014) An approximation algorithm for the unconstrained traveling tournament problem, Annals of Operations Research 218, 237-247.
155: Irnich, S. (2010) A new branch-and-price algorithm for the traveling tournament problem, European Journal of Operational Research 204, 218-228.
156: Januario, T., Urrutia, S. (2016) A new neighborhood structure for round robin scheduling problems, Computers and Operations Research 70, 127-139.
157: Januario, T., Urrutia, S., Ribeiro, C.C., Werra, D. de (2016) Edge coloring: A natural model for sports scheduling, European Journal of Operational Research 254, 1-8.
158: Januario, T., Urrutia, S., Werra, D. de (2016) Sports scheduling search space connectivity: A riffle shuffle driven approach, Discrete Applied Mathematics 211, 113-120.
159: Jeong, H.M., Kim, S.W., Choi, Y., Kim, A.J., Eun, J., Kim, B.J. (2012) Traveling baseball players' problem in Korea, Journal of the Korean Physical Society 61, 484-492.
160: Keedwell, A.D. (2000) Construction, properties and application of finite neofields, Comment. Math. Univ. Carolinae 41, 283-297.
161: Kendall, G. (2008) Scheduling English football fixtures over holiday periods, Journal of the Operational Research Society 59, 743-755.
162: Kendall, G., Knust, S., Ribeiro, C.C., Urrutia, S. (2010) Scheduling in sports: An annotated bibliography, Computers and Operations Research 37, 1-19.
163: Kendall, G., Miserez, W., Vanden Berghe, G. (2006) A constructive heuristic for the traveling tournament problem, in: E. Burke and H. Rudova (eds.), PATAT 2006, Proceedings, 443-447.
164: Kendall, G., McCollum, B., Cruz, F.R., McMullan, P., While, L. (2013) Scheduling English football fixtures: consideration of two conflicting objectives, Hybrid Metaheuristics, Studies in Computational Intelligence 434, 369-385.
165: Kendall, G., Westphal, S. (2013) Sports Scheduling: Minimizing travel for English football supporters, Automated Scheduling and Planning, Studies in Computational Intelligence 505, 61-90.
166: Kern, W., Paulusma, D. (2001) The new FIFA rules are hard complexity aspects of sports competitions, Discrete Applied Mathematics 108, 317-323.
167: Kern, W., Paulusma, D. (2004) The computational complexity of the elimination problem in generalized sports competitions, Discrete Optimization 1, 205-214.
168: Khelifa, M., Boughaci, D. (2015) A variable neighborhood search method for solving the traveling tournaments problem, Electronic Notes in Discrete Mathematics 47, 157-164.
169: Kidd, M.P. (2010) A tabu-search for minimising the carry-over effects value of a round-robin tournament, ORiON 26, 125-141.
170: Kim, T. (2019) Optimal approach to game scheduling of multiple round-robin tournament: Korea professional baseball league in focus, Computers and Industrial Engineering 136, 95-105.
171: Kirkman, T.P. (1847) On a problem in combinations, Cambridge and Dublin Mathematics Journal 2,191-204.
172: Knust, S. (2008) Scheduling sports tournaments on a single court minimizing waiting times, Operations Research Letters 36, 471-476.
173: Knust, S. (2010) Scheduling non-professional table-tennis leagues, European Journal of Operational Research 200, 358-367.
174: Knust, S., Lücking, D. (2009) Minimizing costs in round robin tournaments with place constraints, Computers and Operations Research 36, 2937-2943.
175: Knust, S., Thaden, M. von (2006) Balanced home-away assignments, Dicrete Optimization 3, 354-365.
176: Ko, Y.D., Jung, S.H., Kim, S.H., Lee, S.W. (2018) Sustainable sport scheduling approach considering team equity for the Korean professional baseball league, Sustainability, 10, 429.
177: Kostuk, K.J. (1997) A decision support system for a large, multi-event tournament, INFOR 35, 183-195.
178: Kostuk, K.J., Willoughby, K.A. (2012) A decision support system for scheduling the Canadian football league, Interfaces 42, 286-295.
179: Kujansuu, E., Lindberg, T., Mäkinen, E. (1999) The stable roommates problem and chess tournament pairings, Divulgaciones Matematicas 7, 19-28.
180: Kyngäs, J., Nurmi, K., Kyngäs, N., Lilley, G., Salter, T. (2017) Scheduling the Australian Football League, Journal of the Operational Research Society 68, 973-982.
181: Lambrechts, E., Ficker, A.M., Goossens, D.R., Spieksma, F.C. (2018) Round-robin tournaments generated by the circle method have maximum cartexry-over, Mathematical Programming B 172, 277-302.
182: Lamken, E.R. (1990) Generalized balanced tournament designs, Transactions of the American Mathematical Society 318, 473-490.
183: Lamken, E.R. (1996) A few more partitioned balanced tournament designs, Ars Combinatoria 43, 121-134.
184: Lamken, E.R. (1997) The existence of partitioned generalized balanced tournament designs with block size 3, Designs, Codes and Cryptography 11, 37-71.
185: Lamken, E.R., Vanstone, S.A. (1985) The existence of factored balanced tournament designs, Ars Combinatoria 19, 157-160.
186: Lamken, E.R., Vanstone, S.A. (1987) The existence of partitioned balanced tournament designs, Annals of Discrete Mathematics 34, 339-352.
187: Lamken, E.R., Vanstone, S.A. (1988) Orthogonal resolutions in odd balanced tournament designs, Graphs and Combinatorics 4, 241-255.
188: Lamken, E.R., Vanstone, S.A. (1989) Balanced tournament designs and related topics, Discrete Mathematics 77, 159-176.
189: Larson, J., Johansson, M. (2014) Constructing schedules for sports leagues with divisional and round-robin tournaments, Journal of Quantitative Analysis in Sports 10, 119-129.
190: Lee, J.H., Lee, Y.H., Lee, Y.H. (2006) Mathematical modeling and tabu search heuristic for the traveling tournament problem, in: M.Gavrilova et al. (eds.): ICCSA 2006, Lecture Notes in Computer Science 3982, Springer, 875-884.
191: Lester, M.M. (2022) Pseudo-Boolean optimisation for RobinX sports timetabling, Journal of Scheduling 25, 287–299.
192: Lewis, R., Thompson. J. (2011) On the application of graph colouring techniques in round-robin sports scheduling, Computers and Operations Research 38, 190-204.
193: Lim, A., Zhang, X. (2003) Integer programming and simulated annealing for scheduling sports competition on multiple venues, Proceedings MIC 2003.
194: Lim, A., Rodrigues, B., Zhang, X. (2006) A simulated annealing and hill-climbing algorithm for the traveling tournament problem, European Journal of Operational Research 174, 1459-1478.
195: Lim, A., Rodrigues, B., Zhang, X. (2006) Scheduling sports competitions at multiple venues – revisited, European Journal of Operational Research 175, 171-186.
196: Liu, K., Löffler, S., Hofstedt, P. (2018) Solving the traveling tournament problem with predefined venues by parallel constraint programming, Lecture Notes in Artificial Intelligence 11308, 64-79.
197: Mancini, S., Isabello, A. (2014) Fair referee assignment for the Italian soccer serieA, Journal of Quantitative Analysis in Sports, 10, 153-160.
198: McAloon, K., Tretkoff, C., Wetzel, G. (1997) Sports league scheduling, in: Proceedings of the 3rd ILOG Optimization Suite International Users Conference, Paris.
199: Melo, R.A., Urrutia, S., Ribeiro, C.C. (2007) Scheduling single round robin tournaments with fixed venues, in: Proceedings of the 3rd Multidisciplinary International Conference on Scheduling: Theory and Applications (MISTA'07), 431-438, Paris.
200: Melo, R.A., Urrutia, S., Ribeiro, C.C. (2009) The traveling tournament problem with predefined venues, Journal of Scheduling 12, 607-622.
201: Mendelsohn, E., Rosa, A. (1985) One-factorizations of the complete graph – a survey, Journal of Graph Theory 9, 43-65.
202: Mendelsohn, E., Rodney, P. (1994) The existence of court balanced tournament designs, Discrete Mathematics 133, 207-216.
203: Mitchell, J.E. (2000) Realignment in the national football league, Working Paper, Mathematical Sciences, Rensselaer Polytechnic Institute Troy, NY 12180.
204: Miyashiro, R., Iwasaki, H., Matsui, T. (2003) Characterizing feasible pattern sets with a minimum number of breaks, in: E. Burke and P. De Causmaecker (eds.), PATAT 2002, Lecture Notes in Computer Science 2740, Springer, 78-99.
205: Miyashiro, R., Matsui, T. (2005) A polynomial-time algorithm to find an equitable home-away assignment, Operations Research Letters 33, 235-241.
206: Miyashiro, R., Matsui, T. (2006) Semidefinite programming based approaches to the break minimization problem, Computers and Operations Research 33, 1975-1982.
207: Miyashiro, R., Matsui, T. (2006) Minimizing the carry-over effects value in a round-robin tournament, in: E. Burke and H. Rudova (eds.), PATAT 2006, Proceedings, 402-405.
208: Miyashiro, R., Imahori, S., Matsui, T. (2012) An approximation algorithm for the traveling tournament problem, Annals of Operations Research 194, 317-324.
209: Nemhauser, G.L., Trick, M.A. (1998) Scheduling a major college basketball conference, Operations Research 46, 1-8.
210: Noronha, T.F., Ribeiro, C.C., Duran, G., Souyris, S., Weintraub, A. (2007) A branch-and-cut algorithm for scheduling the highly-constrained Chilean soccer tournament, Lecture Notes in Computer Science 3867, Springer, 174-186.
211: Nowak, M., Epelman, M., Pollock, S.M. (2006) Assignment of swimmers to dual meet events, Computers and Operations Research 33, 1951-1962.
212: Nurmi, K., Goossens, D., Bartsch, T., Bonomo, F., Briskorn, D., Duran, G, Kyngäs, J., Marenco, J., Ribeiro, C., Spieksma, F.., Urrutia, S., Wolf, R. (2010) A framework for a highly constrained sports scheduling problem, Proceedings of the International Multi-Conference of Engineers and Computer Scientists, Volume III, Hong-Kong, 1991-1997
also
IAENG Transactions on Engineering Technologies, American Institute of Physics 5, 14-28.
213: Nurmi, K., Kyngäs, J., Goossens, D. (2011) Scheduling a triple round robin tournament for the Finnish national ice hockey league for players under 20, IEEE SSCI 2011 - CISched 2011: 2011 IEEE Symposium on Computational Intelligence in Scheduling, 46-53.
214: Nurmi, K., Kyngäs, J., Goossens, D. (2013) Scheduling a triple round robin tournament with minitournaments for the Finnish national youth ice hockey league, Journal of the Operational Research Society 65, 1770-1779.
215: Nurmi, K., Kyngäs, J., Goossens, D., Kyngäs, N. (2014) Scheduling a professional sports league using the PEAST algorithm, Lecture Notes in Engineering and Computer Science: International MultiConference of Engineers and Computer Scientists, Hong Kong, 1176-1182.
216: Oliveira, L. de, Souza, C.C. de, Yunes, T. (2014) Improved bounds for the traveling umpire problem: A stronger formulation and a relax-and-fix heuristic, European Journal of Operational Research 236, 592-600.
217: Oliveira, L. de, Souza, C.C. de, Yunes, T. (2016) Lower bounds for large traveling umpire instances: New valid inequalities and a branch-and-cut algorithm, Computers and Operations Research 72, 147-159.
218: Panton, D., Bryant, K., Schreuder, J. (2002) Optimisation tools for round-robin and partial round-robin sporting fixtures, Abstracts from the 6th Australian Conference on Mathematics & Computers in Sport, Bond University, Queensland, Australia.
219: Perron, L. (2005) Alternate modelling in sport scheduling, in: P. van Beek (ed.), CP 2005, Lecture Notes in Computer Science 3709, Springer, 797-801.
220: Post, G., Woeginger, G.J. (2006) Sports tournaments, home-away assignments, and the break minimization problem, Discrete Optimization 3, 165-173.
221: Premananda, I.G.A., Tjahyanto, A., Mukhlason, A. (2024) Efficient iterated local search based metaheuristic approach for solving sports timetabling problems of International Timetabling Competition 2021, Annals of Operations Research 343, 411-427.
222: Raack, C., Raymond, A., Schlechte, T., Werner, A. (2014) Standings in sports competitions using integer programming, Journal of Quantitative Analysis in Sports, 10, 131-137.
223: Rasmussen, R.V. (2008) Scheduling a triple round robin tournament for the best Danish soccer league, European Journal of Operational Research 185, 795-810.
224: Rasmussen, R.V., Trick, M.A. (2008) Round robin scheduling – a survey, European Journal of Operational Research 188, 617-636.
225: Rasmussen, R.V., Trick, M.A. (2007) A Benders approach for the constrained minimum break problem, European Journal of Operational Research 177, 198-213.
226: Rasmussen, R.V., Trick, M.A. (2009) The timetable constrained distance minimization problem, Annals of Operations Research 171, 45-59.
227: Recalde, D., Torres, R., Vaca, P. (2013) Scheduling the professional Ecuadorian football league by integer programming, Computers and Operations Research 40, 2478-2484.
228: Regin, J.-C. (2001) Minimization of the number of breaks in sports scheduling problems using constraint programming, DIMACS Series in Discrete Mathematics and Theoretical Computer Science 57, 115-130.
229: Ribeiro, C.C. (2012) Sports scheduling: problems and applications, International Transactions in Operational Research 19, 201-226.
230: Ribeiro, C.C., Urrutia, S. (2005) An application of integer programming to playoff elimination in football championships, International Transactions in Operational Research 12, 375-386.
231: Ribeiro, C.C., Urrutia, S. (2004) OR on the ball: applications in sports scheduling and management, OR/MS Today 31, 50-54.
232: Ribeiro, C.C., Urrutia, S. (2006) Scheduling the Brazilian soccer championship, in: E. Burke and H. Rudova (eds.), PATAT 2006, Proceedings, 481-483.
233: Ribeiro, C.C., Urrutia, S. (2007) Scheduling the Brazilian soccer tournament with fairness and broadcast objectives, Lecture Notes in Computer Science 3867, Springer, 149-159.
234: Ribeiro, C.C., Urrutia, S. (2007) Heuristics for the mirrored traveling tournament problem, European Journal of Operational Research 179, 775-787.
235: Ribeiro, C.C., Urrutia, S. (2012) Scheduling the Brazilian soccer tournament: solution approach and practice, Interfaces 42, 260-272.
236: Robinson, L.W. (1991) Baseball playoff elimination: an application of linear programming, Operations Research Letters 10, 67-74.
237: Rodney, P. (1995) The existence of interval-balanced tournament designs, Journal of Combinatorial Mathematics and Combinatorial Computing 19, 161-170.
238: Rosa, A., Wallis, W. (1982) Premature sets of 1-factors or how not to schedule round robin tournaments, Discrete Applied Mathematics 4, 217-226.
239: Rosati, R.M., Petris, M., Di Gaspero, L., Schaerf, A. (2022) Multi-neighborhood simulated annealing for the sports timetabling competition ITC2021, Journal of Scheduling 25, 301–319.
240: Russell, K.G. (1980) Balancing carry-over effects in round robin tournaments, Biometrika 67, 127-131.
241: Russell, R.A., Leung, J.M. (1994) Devising a cost effective schedule for a baseball league, Operations Research 42, 614-625.
242: Russell, R.A., Urban, T.L. (2006) A constraint programming approach to the multiple-venue sport-scheduling problem, Computers and Operations Research 33, 1895-1906.
243: Russell, T., van Beek, P. (2012) A hybrid constraint programming and enumeration approach for solving NHL playoff qualification and elimination problems, European Journal of Operational Research 218, 819-828.
244: Sakaguchi, T., Ishizaki, S. (2005) A neural network model for sports scheduling problems with considering travel cost, Transactions of Information Processing Society of Japan 46, 103-110.
245: Saur, M.C., Starr, K., Husted, M., Newman, A.M. (2012) Scheduling softball series in the Rocky Mountain athletic conference, Interfaces 42, 296-309.
246: Schaerf, A. (1999) Scheduling sport tournaments using constraint logic programming, Constraints 4, 43-65.
247: Schauz, U. (2016) The tournament scheduling problem with absences, European Journal of Operational Research 254, 746-754.
248: Schellenberg, P.J., van Rees, G.H.J., Vanstone, S.A. (1977) The existence of balanced tournament designs, Ars Combinatoria 3, 303-318.
249: Schönberger, J., Mattfeld, D.C., Kopfer, H. (2000) Automated timetable generation for rounds of a table-tennis league, Proceedings of the 2000 Congress on Evolutionary Computation, 277-284.
250: Schönberger, J., Mattfeld, D.C., Kopfer, H. (2004) Memetic algorithm timetabling for non-commercial sport leagues, European Journal of Operational Research 153, 102-116.
251: Schreuder, J.A.M. (1980) Constructing timetables for sport competitions, Mathematical Programming Study 13, 58-67.
252: Schreuder, J.A.M. (1992) Combinatorial aspects of construction of competition dutch professional football leagues, Discrete Applied Mathematics 35, 301-312.
253: Schreuder, J.A.M. (1993) Construction of fixture lists for professional football leagues, Ph.D. thesis, University of Strathclyde, Glasgow.
254: Straley, T.H. (1983) Scheduling designs for a league tournament, Ars Combinatoria 15, 193-200.
255: Su, L.-H., Chiu, Y., Cheng, T.C.E. (2013) Sports tournament scheduling to determine the required number of venues subject to the minimum timeslots under given formats, Computers and Industrial Engineering 65, 226-232.
256: Suksompong, W. (2016) Scheduling asynchronous round-robin tournaments, Operations Research Letters 44, 96-100.
257: Suzuka, A., Miyashiro, R., Yoshise, A., Matsui, T. (2005) Semidefinite programming based approaches to home-away assignment problems in sports scheduling, The First International Conference on Algorithmic Applications in Management (AAIM 2005), Lecture Notes in Computer Science 3521, Springer, 95-103.
258: Suzuka, A., Miyashiro, R., Yoshise, A., Matsui, T. (2006) Dependent randomized rounding to the home-away assignment problem in sports scheduling, IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol.E89-A, 1407-1416.
259: Suzuka, A., Miyashiro, R., Yoshise, A., Matsui, T. (2007) The home-away assignment problems and break minimization/maximization problems in sports scheduling, Pacific Journal of Optimization 3, 113-133.
260: Suzuka, A., Saruwatari, Y., Yoshise, A. (2002) Solving sports scheduling problems using network structure, Proceedings PATAT 2002, KaHo Sint-Lieven, Gent, Belgium.
261: Tajbakhsh, A., Eshghi, K., Shamsi, A. (2012) A hybrid PSO-SA algorithm for the travelling tournament problem, European Journal of Industrial Engineering 6, 2-25.
262: Thielen, C., Westphal, S. (2011) Complexity of the traveling tournament problem, Theoretical Computer Science 412, 345-351.
263: Thielen, C., Westphal, S. (2012) Approximation algorithm for TTP(2), Mathematical Methods of Operations Research 76, 1-20.
264: Toffolo, T., Christiaens, J., Spieksma, F.C.R., Vanden Berghe, G. (2019) The sport teams grouping problem, Annals of Operations Research 275, 223-243.
265: Toffolo, T., Wauters, T., Van Malderen, S., Vanden Berghe, G. (2016) Branch-and-bound with decomposition-based lower bounds for the traveling umpire problem, European Journal of Operational Research 250, 737-744.
266: Trick, M.A. (2001) A schedule-then-break approach to sports timetabling, in: E. Burke and W. Erben (eds.), PATAT 2000, Lecture Notes in Computer Science 2079, Springer, 242-252.
267: Trick, M.A. (2003) Integer and constraint programming approaches for round-robin tournament scheduling, in: E. Burke and P. De Causmaecker (eds.), PATAT 2002, Lecture Notes in Computer Science 2740, Springer, 63-77.
268: Trick, M.A. (2004) Using sports scheduling to teach integer programming, INFORMS Transactions on Education 5, 10-17.
269: Trick, M.A., Yildiz, H. (2007) Bender's cuts guided large neighborhood search for the traveling umpire problem, Lecture Notes in Computer Science 4510, 332-345.
270: Trick, M.A., Yildiz, H. (2011) Benders' cuts guided large neighborhood search for the traveling umpire problem, Naval Research Logistics 58, 771-781.
271: Trick, M.A., Yildiz, H. (2012) Locally optimized crossover for the traveling umpire problem, European Journal of Operational Research 216, 286-292.
272: Trick, M.A., Yildiz, H., Yunes, T. (2012) Scheduling major league baseball umpires and the traveling umpire problem, Interfaces 42, 232-244.
273: Triska, M., Musliu, N. (2012) An effective greedy heuristic for the social golfer problem, Annals of Operations Research 194, 413-425.
274: Triska, M., Musliu, N. (2012) An improved SAT formulation for the social golfer problem, Annals of Operations Research 194, 427-438.
275: Urban, T.L., Russell, R.A. (2003) Scheduling sports competitions on multiple venues, European Journal of Operational Research 148, 302-311.
276: Urrutia, S., Ribeiro, C.C. (2006) Maximizing breaks and bounding solutions to the mirrored traveling tournament problem, Discrete Applied Mathematics 154, 1932-1938.
277: Urrutia, S., Ribeiro, C.C., Melo, R.A. (2007) A new lower bound to the traveling tournament problem, in: Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Scheduling (CI-Sched 2007), Honolulu, 15-18.
278: Urrutia, S., Werra, D. de, Januario, T. (2021) Recoloring subgraphs of $K_{2n}$ for sports scheduling, Theoretical Computer Science 877, 36–45.
279: Uthus, D.C., Riddle, P.J., Guesgen, H.W. (2008) Ant colony optimization and the single round robin maximum value problem, Lecture Notes in Computer Science 5217, ANTS 2008, Springer, 243-250.
280: Uthus, D.C., Riddle, P.J., Guesgen, H.W. (2009) An ant colony optimization approach to the traveling tournament problem, Proceedings GECCO 2009, Montreal.
281: Uthus, D.C., Riddle, P.J., Guesgen, H.W. (2009) DFS* and the traveling tournament problem, Lecture Notes in Computer Science 5547, CPAIOR 2009, Springer, 279-293.
282: Uthus, D.C., Riddle, P.J., Guesgen, H.W. (2012) Solving the traveling tournament problem with iterative-deepening A 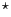$^\star$ , Journal of Scheduling 15, 601-614.
283: Van Bulck, D., Goossens, D., Spieksma, F.C.R. (2019) Scheduling a non-professional indoor football league: a tabu search based approach, Annals of Operations Research 275, 715-730.
284: Van Bulck, D., Goossens, D. (2020) Handling fairness issues in time-relaxed tournaments with availability constraints, Computers and Operations Research 115, 104856.
285: Van Bulck, D., Goossens, D. (2020) On the complexity of pattern feasibility problems in time-relaxed sports timetabling, Operations Research Letters 48, 452-459.
286: Van Bulck, D., Goossens, D., Schönberger, J., Guajardo, M. (2020) RobinX: A three-field classification and unified data format for round-robin sports timetabling, European Journal of Operational Research 280, 568-580.
287: Van Bulck, D., Goossens, D. (2022) Optimizing rest times and differences in games played: an iterative two-phase approach, Journal of Scheduling 25, 261-271.
288: Van Bulck, D., Goossens, D. (2023) First-break-heuristically-schedule: Constructing highly-constrained sports timetables, Operations Research Letters 51 (2023) 326-331.
289: Van Bulck, D., Goossens, D. (2023) A traditional Benders’ approach to sports timetabling, European Journal of Operational Research 307, 813–826.
290: Van Bulck, D., Goossens, D. (2023) The international timetabling competition on sports timetabling (ITC2021), European Journal of Operational Research 308, 1249–1267.
291: Van Bulck, D., Goossens, D., Clarner, J.-P., Dimitsas, A., Fonseca, G.H.G., Lamas-Fernandez, C., Lester, M.M., Pedersen, J., Phillips, A.E., Rosati, R.M. (2024) Which algorithm to select in sports timetabling? European Journal of Operational Research 318, 575–591.
292: Van Doornmalen, J., Hojny, C., Lambers, R., Spieksma, F.C.R. (2023) Integer programming models for round robin tournaments, European Journal of Operational Research 310, 24-33.
293: Van Voorhis, T.V. (2002) Highly constrained college basketball scheduling, Journal of the Operational Research Society 53, 603-609.
294: Van Voorhis, T.V. (2005) College basketball scheduling with travel swings, Computers and Industrial Engineering 48, 163-172.
295: van't Hof, P., Post, G., Briskorn, D. (2010) Constructing fair round robin tournaments with a minimum number of breaks, Operations Research Letters 38, 592-596.
296: Wallis, W.D. (1983) A tournament problem, Journal of the Mathematical Society, Series B 24, 289-291.
297: Walser, J.P. (1999) Integer optimization by local search – a domain-independent approach, Lecture Notes in Artificial Intelligence 1637, Springer, Berlin-Heidelberg.
298: Wang, W., Xue, F., Mitsui, T., Shang, Z., Shigeno, M. (2024) Carry-over effect values minimization under circle method and binary factorization based on Jaya algorithm, Proceedings of the 8th International Conference on Control Engineering and Artificial Intelligence, 44-51.
299: Wauters, T., Van Malderen, S., Vanden Berghe, G. (2014) Decomposition and local search based methods for the traveling umpire problem, European Journal of Operational Research 238, 886-898.
300: Wayne, K. (2001) A new property and a faster algorithm for baseball elimination, SIAM Journal on Discrete Mathematics 14, 223-229.
301: Weert, A. van, Schreuder, J.A.M. (1998) Construction of basic match schedules for sports competitions by using graph theory, in: E. Burke and M. Carter (eds.), PATAT 1997, Lecture Notes in Computer Science 1408, Springer, 201-210.
302: Werners, B., Wülfing, T. (2007) Optimierung von Spielplänen am Beispiel der Fussball-Bundesliga-Saison 2006/07, Zeitschrift für Planung & Unternehmenssteuerung 18, 207-221.
303: Werra, D. de (1980) Geography, games, and graphs, Discrete Applied Mathematics 2, 327-337.
304: Werra, D. de (1981) Scheduling in sports, in: P. Hansen (ed.), Studies on Graphs and Discrete Programming, 381-395.
305: Werra, D. de (1982) Minimizing irregularities in sports schedules using graph theory, Discrete Applied Mathematics 4, 217-226.
306: Werra, D. de (1985) On the multiplication of divisions: the use of graphs for sports scheduling, Networks 15, 125-136.
307: Werra, D. de (1988) Some models of graphs for scheduling sports competitions, Discrete Applied Mathematics 21, 47-65.
308: Werra, D. de, Descombes, J.L., Masson, P. (1990) A constrained sports scheduling problem, Discrete Applied Mathematics 26, 41-49.
309: Werra, D. de, Ekim, T., Raess, C. (2006) Construction of sports schedules with multiple venues, Discrete Applied Mathematics 154, 47-58.
310: Westphal, S. (2014) Scheduling the German basketball league. Interfaces, 44, 498-508.
311: Westphal, S., Noparlik, K. (2014) A 5.875-approximation for the traveling tournament problem, Annals of Operations Research 218, 347-360.
312: While, L., Kendall, G. (2014) Scheduling the English football league with a multi-objective evolutionary algorithm. International Conference on Parallel Problem Solving from Nature, Lecture Notes in Computer Science 8672, Springer, 842-851.
313: Willis, R.J., Terrill, B.J. (1994) Scheduling the Australian state cricket season using simulated annealing, Journal of the Operational Research Society 45, 276-280.
314: Wright, M. (1991) Scheduling English cricket umpires, Journal of the Operational Research Society 42, 447-452.
315: Wright, M. (1992) A fair allocation of county cricket opponents, Journal of the Operational Research Society 43, 195-201.
316: Wright, M. (1994) Timetabling county cricket fixtures using a form of tabu search, Journal of the Operational Research Society 45, 758-770.
317: Wright, M. (2005) Scheduling fixtures for New Zealand cricket, IMA Journal of Management Mathematics 16, 99-112.
318: Wright, M. (2006) Scheduling fixtures for basketball New Zealand, Computers and Operations Research 33, 1875-1893.
319: Wright, M. (2009) 50 years of OR in sport, Journal of the Operational Research Society 60, 161-168.
320: Wright, M. (2018) Scheduling an amateur cricket league over a nine-year period, Journal of the Operational Research Society, 69, 1854-1862.
321: Xiao, M., Kou, S. (2016) An improved approximation algorithm for the traveling tournament problem with maximum trip length two, 41st International Symposium on Mathematical Foundations of Computer Science (MFCS 2016), Leibniz International Proceedings in Informatics, Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 89:1-89:14,
322: Xue, L., Luo, Z., Lim, A. (2015) Two exact algorithms for the traveling umpire problem, European Journal of Operational Research 243, 932-943.
323: Yang, J.T., Huang, H.-D., Yang, J., Horng, J.-T. (1999) Devising a cost effective baseball scheduling by evolutionary algorithms, Working Paper, Department of Computer Science and Information Engineering, National Central University, Chungli 32054, Taiwan.
324: Yamaguchi, D., Imahori, S., Miyashiro, R., Matsui, T. (2009) An improved approximation algorithm for the traveling tournament problem, Lecture Notes in Computer Science 5878, Springer, 679-688.
325: Yamaguchi, D., Imahori, S., Miyashiro, R., Matsui, T. (2011) An improved approximation algorithm for the traveling tournament problem, Algorithmica 61, 1077-1091.
326: Yavuz, M., Inan, U.H., Figlali, A. (2008) Fair referee assignments for professional football leagues, Computers and Operations Research 35, 2937-2951.
327: Yi, X., Goossens, D., Nobibon, F.T. (2020) Proactive and reactive strategies for football league timetabling, European Journal of Operational Research 282, 772-785.
328: Yi, X., Goossens, D. (2023) Strategies for dealing with uncertainty in time-relaxed sports timetabling, Annals of Operations Research 320, 473–492.
329: Zeng, L., Mizuno, S. (2012) On the separation in 2-period double round robin tournaments with minimum breaks, Computers and Operations Research 39, 1692-1700.
330: Zeng, L., Mizuno, S. (2013) Constructing fair single round robin tournaments regarding strength groups with a minimum number of breaks, Operations Research Letters 41, 506-510.
331: Zhao, J., Xiao, M. (2025) A 5-approximation algorithm for the traveling tournament problem, Annals of Operations Research 346, 2287–2305.