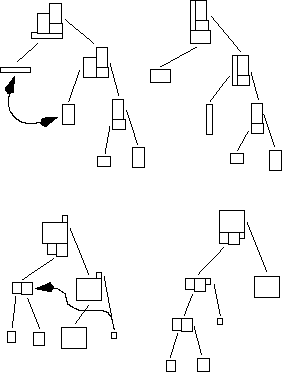
Figure 7: Mutation by exchaning blocks (top) and by changing the structure of slicing tree (bottom)
After the construction of the initial individuals, which already contain
a lot of good components, the genetic algorithm starts the optimization
by modifying individuals (mutation), and by
combining building-blocks (crossover).
Beside a mutation operator for changing the arrangement of two blocks inside
a meta-block, the main mutation operators modify
the slicing tree (cf. fig. 7).
One operator exchanges blocks or meta-blocks,
which corresponds to exchanging cells or partial layouts on
the layout surface.
The other important mutation operator changes the structure of the tree
by randomly picking out a subtree and inserting it into the tree at a
different position, which corresponds to moving cells or partial layouts
on the layout surface.
Here storing all important implementations for the meta-blocks once more enhances
the performance of the genetic algorithm, because for a moved
partial layout a different implementation might be better in its
new environment.
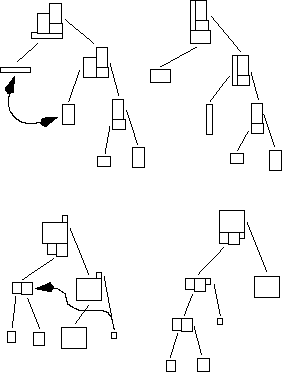
Figure 7: Mutation by exchaning blocks (top) and by changing
the structure of slicing tree (bottom)
The implementation of the crossover operator is straight-forward:
Two individuals are randomly chosen to produce one offspring.
Two disjunct subtrees are searched in the parents which are
composed to a subtree in the offspring.
Because these subtrees usually do not build a complete layout,
a third part has to be added to the layout of the resulting
offspring.
Due to this, the heritability (number of transmitted genes
from the parents) is smaller than for
problems where crossing-over directly leads to a correct
individual.
During the adding of the missing blocks into the tree of the
offspring, the iterated matching is used once more to construct
new (good) building-blocks.
It has turned out to be not helpful to do some `intelligent'
crossover, i. e. looking for large disjunct subtrees, for example.
Research is carried out to include a recombination operator
for gene pool recombination.
Here an offspring is constructed by combining building-blocks
out of a pool of good partial solutions.
When designing a genetic algorithm for a specific problem, it is very important that a global optimum can be reached starting from any set of individuals by the application of the genetic operators. For an algorithm with tree-structured genotype encoding this means, if recombination only combines real subtrees with at least two leaves, then each pair of leaves contained in the encoding of an optimal solution must already exist in one of the initial individuals, or must be able to be constructed by mutation. Otherwise the genetic algorithm will never reach the optimum.