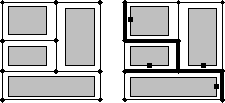
Figure 3: A routing graph (left) and a global route for a four terminal net (right)
The aim of the routing phase is to find the geometrical layouts for all nets.
In the floorplanning phase space on the layout surface has been provided to
complete the interconnections.
This space can be described as a collection of single routing regions.
Each region has a fixed capacity, i.e. a maximum number of wires which
can be routed through this region, and a number of terminals, i.e.\
pins on the borders of the adjacent cells.
Due to the complexity, the routing is done in two sub-phases. In the global routing, the `loose' routes for the nets are determined. For the computation of the global routing, the routing space is represented as a graph, the edges of this graph represent the routing regions and are weighted with the corresponding capacities (cf. fig. 3). The global routing is described by a list of routing regions for each net of the circuit, with none of the capacities of any routing region being exceeded.

Figure 3: A routing graph (left) and a global route for a four terminal net (right)
After global routing is done, for each routing region the number of nets routed through it is known. In the detailed routing phase the exact routes for the wires have to be determined (figure 4). This is done incrementally, i.e. one channel is routed at a time in a predefined order.
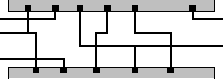
Figure 4: The detailed routing inside a channel
The global routing can be solved by graph based techniques, Integer Programming or hierarchical approaches [5]. For the detailed routing there exist solutions based on Greedy Methods, graph algorithms or hierarchical approaches [9]. The complexity and routability of a layout depends on the number of layers which can be used for the completion of the interconnections. Usually in macro cell layout there are two layers and the routing is done in the manhattan-model, i.e. one layer is for the vertical, the other for the horizontal wires and the nets change the layer when changing their direction.