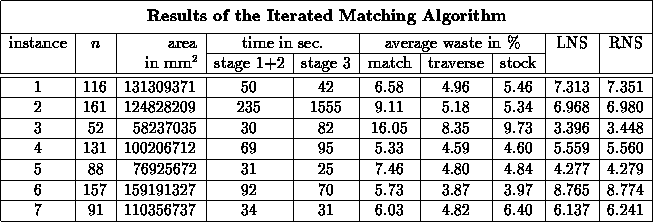
Table 1: Results of the four stage algorithm
The algorithm, programmed in C, has been tested with several instances taken from real demands of a glass factory, containing between 52 and 161 rectangles. A PC-486 (33 MHz) was used to measure the time requirements of the algorithm. The time give information about the real computation time, i.e. requirements for input and output are not considered. The stock rectangles are of dimension about 6000 mm x 3200 mm for all instances. The maximal traverse length is 2300 mm and the minimal cut distance is 20 mm for all instances except instance three. Here the minimal cut distance is 40 mm since the thickness of the required stock sheet is 6 mm and not 4 mm as it is for the other instances.

Table 1: Results of the four stage algorithm
Table 1 shows the data of the instances and the computational
results of the four stage algorithm discussed in section six.
The number  of the demand rectangles of the instances is given in the second
column and the sum of all demand rectangle area is listed in the third column.
The time column gives information about the time requirements in seconds
of stage one, two and three.
Stage one and two are considered together, because they
both show how fast the iterated matching works.
The time needed to run the modified first fit decreasing is not listed,
because it only takes less than one second.
The match waste is the average waste in percent of all traverses after stage
two, the traverse waste is the waste after stage three and the
stock waste is the average waste of all computed layouts at the
end of the algorithm.
of the demand rectangles of the instances is given in the second
column and the sum of all demand rectangle area is listed in the third column.
The time column gives information about the time requirements in seconds
of stage one, two and three.
Stage one and two are considered together, because they
both show how fast the iterated matching works.
The time needed to run the modified first fit decreasing is not listed,
because it only takes less than one second.
The match waste is the average waste in percent of all traverses after stage
two, the traverse waste is the waste after stage three and the
stock waste is the average waste of all computed layouts at the
end of the algorithm.
The number of the at least needed stock rectangles (LNS) and of the real needed stock rectangles (RNS)
gives information about how good the modified first fit decreasing assigns the
traverses to the stock rectangles. LNS is a lower bound for the number of
required stock rectangles,
RNS is the fractional number of really needed stock rectangles.
LNS and RNS are calculated as follows: Let 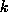 be
the number of traverses after stage three,
be
the number of traverses after stage three, 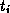 the length of
traverse
the length of
traverse 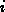 according to the given width
according to the given width 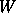 and length
and length 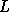 of the stock sheet.
Then
of the stock sheet.
Then
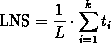
is a lower bound for the number of needed stock sheets.
Notice, that it is not guaranteed that this bound can really be reached.
To calculate RNS, let 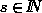 be the number of used stock rectangles
be the number of used stock rectangles
 ,
,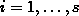 . Assume that
. Assume that 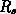 is the stock sheet which is filled
at least in length and let
is the stock sheet which is filled
at least in length and let  denote the used
denote the used  -dimension of
-dimension of 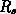 . Then
. Then
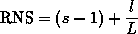
is the fractional number of really needed stock rectangles.
The iterated matching produces traverses with little average waste (about 8 percent) in a very short time. Exceptions are the instances two and three. Here the greedy behaviour of the matching strategy has to be adjusted. This is done in stage three.
The improvement of the traverses in stage three takes in most cases only a few seconds (no more than 95 seconds), except for instance two. If the third stage for solving instance two is considered in detail it can be seen that most of the improvement is done in the first thirty seconds. Hence, a time restriction for stage three would be useful. Notice, that it is not the number of demand rectangles, that makes the algorithm impracticable for instance two. Instance six involves nearly the same number of demand rectangles but it has the smallest waste of all computed instances and it takes only two minutes and 42 seconds to compute this solution.
The modified first fit decreasing finds good solutions for the assignment of the traverses to the stock rectangles. This can be seen in the very small difference between LNS and RNS. Analyzing Table 1, it can be seen that the average waste of all computed layouts is less than six percent and that the time requirement, with exception of instance two, is less than three minutes. Four of the seven instances really take less than 112 seconds for computation.
Hence, we can conclude that the iterated matching is a new efficient method
for solving
the two dimensional cutting stock problem subject to the restrictions
of the industry which is applicable for instances with a large number of rectangles.