 N-puzzle [7],
and partial constraint satisfaction problems [3].
All of them are known to be NP-hard.
N-puzzle [7],
and partial constraint satisfaction problems [3].
All of them are known to be NP-hard.
Previous: Introduction
As an application problem domain, we have chosen the class of discrete optimization problems, which can be defined in terms of finding a solution path in a tree or graph from an initial (root) state to a goal node.
Many applications in planning and scheduling can be
formulated with this model:
the cutting stock problem [2],
the bin packing problem,
vehicle routing,
VLSI floorplan optimization [1,27],
satisfiability problems,
the traveling salesman problem [6],
the N  N-puzzle [7],
and partial constraint satisfaction problems [3].
All of them are known to be NP-hard.
N-puzzle [7],
and partial constraint satisfaction problems [3].
All of them are known to be NP-hard.
For our benchmarks, we have chosen
two typical applications with different solution techniques:
the VLSI floorplan optimization problem, which is solved with
a depth-first branch-and-bound strategy,
and the N  N--puzzle, which is solved with
an iterative-deepening search.
Both are based on depth-first search (DFS),
which traverses the decision tree in a top-down manner from left to right.
DFS is commonly used in combinatorial
optimization problems, because it needs only
N--puzzle, which is solved with
an iterative-deepening search.
Both are based on depth-first search (DFS),
which traverses the decision tree in a top-down manner from left to right.
DFS is commonly used in combinatorial
optimization problems, because it needs only
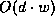 storage space in trees of depth d and width w.
storage space in trees of depth d and width w.