


Next: Parallel Depth-First Search
Up: Applications
Previous: VLSI Floorplan Optimization
Applications with bad initial cost-bounds and many alternatives
in the decision trees are solved with heuristic search algorithms
like A* [11,13] and IDA* [7].
One such example is the
N  N--puzzle [7,11,13].
Here, a given initial configuration of tiles in a squared tray of
size N
N--puzzle [7,11,13].
Here, a given initial configuration of tiles in a squared tray of
size N  N must be
re-arranged with the fewest number of moves into a given goal configuration.
No effective upper cost-bounds are known for this problem,
and hence it cannot be solved with DFBB.
Even the relatively small 15-puzzle (N=4) has a
search space of
N must be
re-arranged with the fewest number of moves into a given goal configuration.
No effective upper cost-bounds are known for this problem,
and hence it cannot be solved with DFBB.
Even the relatively small 15-puzzle (N=4) has a
search space of 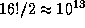 states.
While it would seem easy to obtain any solution, finding an optimal
(=shortest) solution is
states.
While it would seem easy to obtain any solution, finding an optimal
(=shortest) solution is 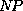 -complete [16].
In general, it takes some hundred million node expansions to solve
a random problem instance of the 15-puzzle, using the Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.
-complete [16].
In general, it takes some hundred million node expansions to solve
a random problem instance of the 15-puzzle, using the Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.
Iterative-deepening A* (IDA*) [7]
simulates a best-first search by a series of depth-first searches
with successively increased cost-bounds.
Its low space overhead of 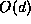 makes it feasible in applications where
A* [11] cannot be used due to memory limitations.
With a non-overestimating heuristic estimate function,
IDA* is guaranteed to find an optimal (shortest) solution [7].
In contrast to DFBB, IDA* halts after finding a first solution, because
optimality is guaranteed by the iterative approach with the minimal
cost-bound increments [7].
makes it feasible in applications where
A* [11] cannot be used due to memory limitations.
With a non-overestimating heuristic estimate function,
IDA* is guaranteed to find an optimal (shortest) solution [7].
In contrast to DFBB, IDA* halts after finding a first solution, because
optimality is guaranteed by the iterative approach with the minimal
cost-bound increments [7].
WWW-Administration
Tue May 16 19:29:30 MET DST 1995
 N--puzzle [7,11,13].
Here, a given initial configuration of tiles in a squared tray of
size N
N--puzzle [7,11,13].
Here, a given initial configuration of tiles in a squared tray of
size N  N must be
re-arranged with the fewest number of moves into a given goal configuration.
No effective upper cost-bounds are known for this problem,
and hence it cannot be solved with DFBB.
Even the relatively small 15-puzzle (N=4) has a
search space of
N must be
re-arranged with the fewest number of moves into a given goal configuration.
No effective upper cost-bounds are known for this problem,
and hence it cannot be solved with DFBB.
Even the relatively small 15-puzzle (N=4) has a
search space of 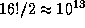 states.
While it would seem easy to obtain any solution, finding an optimal
(=shortest) solution is
states.
While it would seem easy to obtain any solution, finding an optimal
(=shortest) solution is 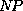 -complete [16].
In general, it takes some hundred million node expansions to solve
a random problem instance of the 15-puzzle, using the Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.
-complete [16].
In general, it takes some hundred million node expansions to solve
a random problem instance of the 15-puzzle, using the Manhattan distance
(the sum of the minimum displacement of each tile from its goal position)
as a heuristic estimate function.
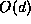 makes it feasible in applications where
A* [
makes it feasible in applications where
A* [