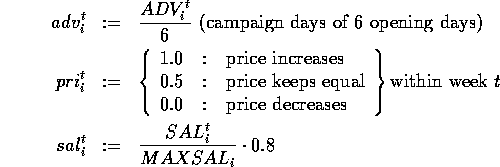
An efficient preprocessing of the data is necessary to input it into the net. All information must be normalized to fit into the interval . We assume that the necessary information is given for T weeks in the past. With the following definitions
|
| ||
|
| ||
|
|
we have decided to use the following inputs for each article i and week t:
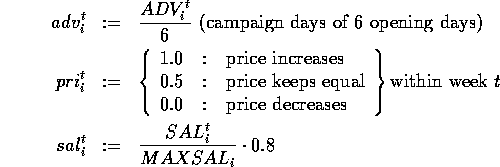
For each article i and recent week t we use a three-dimensional vector:
|
|
For a week t in the future the vector is reduced by the unknown sale:
|
|
To predict the sale for one article within a week t, we use a window of the last n weeks. So we have the following input vector for each article i:
|
|
Because all the considered articles belong to one product group, we have quite a constant sales volume of all products. An increasing sale of one article in general leads to a decrease of the other sales. Due to this, we concatenate the input vectors of all p articles to get the vector given to the input layer:
The sale of article i within week t ( ) is the requested nominal value in the output layer that has to be learned by one net for this vector. So we have p nets and the i-th net adapts the sale behaviour of article i. Therefore we have a training set with the following pairs (see figure 4):
|
|
To forecast the unkown sale for any article i within a future week T+1 we give the following input vector to the trained i-th net:
|
|
The output value of this net is expected to be the value , which has to be re-scaled to the value for the sale of article i within week T+1:
|
|