Artificial neural networks

Artificial neural networks consist of simple calculation elements, called neurons, and weighted connections between them. In a feedforward multilayer perceptron (figure 4) the neurons are arranged in layers and a neuron from one layer is fully connected only to each neuron of the next layer. The first and last layer are the input respectively output layer. The layers between them are called hidden. Values are given to the neurons in the input layer; the results are taken from the output layer. The outputs of the input neurons are propagated through the hidden layers of the net. Figure 3 shows the algorithm each neuron performs.

 
Figure 3:  How a perceptron works

The activation $a$_hj of a hidden or output neuron j is the sum of the incoming data multiplied by the connection weights like in a matrix product. The individual bias value _hj is added to this before the output $o$_hj is calculated by a sigmoid function f:

$o$_hj:= f(a_hj)

f is a bijective function 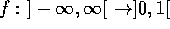because the output has to be $o$_hj∈[0, 1] . We use

$f(a)\; :=\; \{11\; +\; exp(-a)\}.$

Such a feedforward multilayer perceptron can approximate any function after a suitable amount of training. Therefor known discrete values of this function are presented to the net. The net is expected to learn the function rule [2].

 
Figure 4:  Feedforward multilayer perceptron for time series prediction

The behaviour of the net is changed by modification of the weights and bias values. The back-propagation learning algorithms we use to optimize these values is described later together with its parallelizations.