Slicing Trees
Next: Maximum Weight Matching
Up: Cutting Stock by Iterated
Previous: Shape Functions
To store the actual pairs in every iteration step
we use binary slicing trees. Every leaf of a tree represents a demand rectangle,
an interior node of a tree represents a meta rectangle.
Two nodes have the same father if the rectangles represented by these nodes
are paired. In every node the shape function of the corresponding meta rectangle
is stored.
A slicing tree is built bottom up.
At the beginning of the algorithm all slicing trees consist of only one node
(the root) representing the demand rectangles. In every iteration step,
some of the trees are combined by a common father, which is the root
of a new slicing tree representing the new meta rectangle.
The iteration stops, if no more suitable
pairs can be matched. A detailed description of this stop criteria is given
in section six.
Since all nodes contain a shape function and every
shape function describes all possible layouts of a meta rectangle, the slicing
trees contain an exponential number of possible layouts for the stock
rectangles.
When the algorithm has ended, we can detect how the demand rectangles
should be cut out of the stock rectangles. Therefore, a tree is traversed
in top down order.
Since every node stores a shape function we can detect how the first
cut in the stock rectangle has to be made by considering the shape
function in the root of a tree and searching for the first slicing
instruction whose 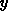 -value is smaller or equal to the width of the
stock rectangle. Due to the property of the shape functions mentioned above, we
automatically get the slicing instruction which describes the layout with
the minimal length according to the made pairings. If the first cut has been
carried out, the stock rectangle is split into two parts.
The shape functions in the sons of the root describe how these two parts
efficiently have to be split further. This proceeding is shown
in Figure 5 by an example. By the traversal of all slicing trees
(one slicing tree for every layout) the demand rectangles can be produced.
-value is smaller or equal to the width of the
stock rectangle. Due to the property of the shape functions mentioned above, we
automatically get the slicing instruction which describes the layout with
the minimal length according to the made pairings. If the first cut has been
carried out, the stock rectangle is split into two parts.
The shape functions in the sons of the root describe how these two parts
efficiently have to be split further. This proceeding is shown
in Figure 5 by an example. By the traversal of all slicing trees
(one slicing tree for every layout) the demand rectangles can be produced.

Figure 5: Layout and corresponding slicing tree
Next: Maximum Weight Matching
Up: Cutting Stock by Iterated
Previous: Shape Functions
Andreas Fritsch
Mon Dec 19 14:08:31 MET 1994
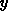 -value is smaller or equal to the width of the
stock rectangle. Due to the property of the shape functions mentioned above, we
automatically get the slicing instruction which describes the layout with
the minimal length according to the made pairings. If the first cut has been
carried out, the stock rectangle is split into two parts.
The shape functions in the sons of the root describe how these two parts
efficiently have to be split further. This proceeding is shown
in Figure 5 by an example. By the traversal of all slicing trees
(one slicing tree for every layout) the demand rectangles can be produced.
-value is smaller or equal to the width of the
stock rectangle. Due to the property of the shape functions mentioned above, we
automatically get the slicing instruction which describes the layout with
the minimal length according to the made pairings. If the first cut has been
carried out, the stock rectangle is split into two parts.
The shape functions in the sons of the root describe how these two parts
efficiently have to be split further. This proceeding is shown
in Figure 5 by an example. By the traversal of all slicing trees
(one slicing tree for every layout) the demand rectangles can be produced.
