subject to
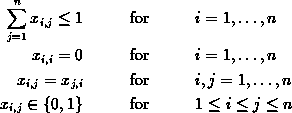
To find out in every iteration step, which of the available rectangles have to be paired, a maximum weight matching in a complete undirected weighted graph is used. The nodes of the graph represent the available (meta) rectangles, the edges represent the possible pairs and the weights give information about the benefit of a pair. The higher the weight, the better the pair. The weights are found by a so called benefit function, which evaluates the possible pairing of two rectangles by considering the corresponding shape functions. For example, a possible benefit function for the pairing of two rectangles is to calculate the average waste of all possible layouts of the resulting meta rectangle and to subtract this value from 100. This encourages the formation of meta rectangles having many densely packed layouts. If all weights of the edges are calculated, the maximum weight matching finds the set of edges, which maximizes the sum of all weights under the constraint that no two edges are adjacent.
This problem can be formulated as a LP-problem as follows:
MaximizeHere,
subject to
is the number of available meta rectangles and 
is the cost matrix.
The value of 
is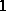 
if the rectangles 
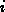and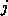 
are matched and
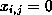if not.
Edmonds showed, that the
maximum weight matching problem can be solved in time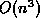 
.
The algorithm used in this application was suggested by Gabow [Gab 1973].
Figure 6 shows the matching algorithm for seven rectangles
in three iteration steps. The edges with zero benefit are not shown.
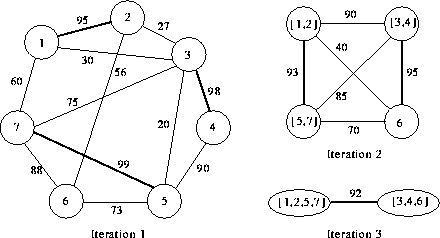
Figure 6: Maximum weight matching in three iterations